佐藤舞先生によるデータ活用講座 Lesson3「データ活用に役立つ統計学ってどんなもの?」

講師:佐藤舞さん
▼プロフィール
佐藤 舞(さとう まい)。データ活用コンサルタント。合同会社デルタクリエイトの代表社員であり、マーケティング・サイエンス学会に所属。データ活用や統計学の入門書籍として出版した『はじめての統計学 レジの行列が早く進むのは、どっち!?』(総合法令出版)は、多くの書店ランキングで1位を獲得。
※役職や所属は取材時のものです。
佐藤舞先生によるLESSON1 解説動画
データ活用に役立つ統計学ってどんなもの?
前回までのレッスンでは、データ活用のメリットやポイント、データ分析方法の概要について解説しました。今回のレッスンでは、データを基にしたコミュニケーションでビジネスを進めていく際の共通言語となる、最低限の統計学の基礎知識について解説していきます。今回のレッスンのゴールは、
- 敷居の高い統計学を直感的に理解する
- データ活用に最低限必要な共通言語を身につける
の2つです。
社内でデータを扱う役割を任されたけれど、入門書を読んだり大学の講義を受けたり、セミナーに参加しても挫折してしまうケースは非常に多いです。そのため今回のレッスンでは、まずは統計学を直感的に理解した上で、必要最低限の共通言語を身につけることを目的としています。そして、この「最低限」というのが実は本質的な部分です。ここさえ押さえておけば会話をするために必要なポイントは身につけることができるので、ぜひきちんとインプットしていただければと思います。
1. 統計学は何の役に立つのか
統計学を学び始めたのはいいけれど、その途中で「そもそもこれって何の役に立つのだろう?」という疑問が湧いてくる方は非常に多いです。そこで統計学の基礎知識についてお話しする前に、どういった場面で統計学の力が発揮されるのか、ビジネスの文脈に絡めてお話していきます。
統計学の役割は、以下の2つに分けられます。
- 自然現象、社会現象を問わず、多くの現象を観測(調査、実験など)して得られる数値的データを分析することで、その現象になんらかの法則性を見出す
- 客観性が高いため、分野を問わず主張の根拠として利用する
データや数字を基に、どのような意思決定をすべきか判断軸をつくるのが統計学の役割です。組織全体でコンセンサスを取って、自信を持って意思決定をするための羅針盤のような存在と捉えていただければと思います。
統計学が役立つ具体的なビジネスシーンについて例を上げてみましょう。社内で「この施策を打てば売上が上がると思います」というようなプレゼンをする場面はよくあると思います。その際「いいアイディアだけど、根拠あるの?」と聞かれて「やってみないと分かりません」としか答えられない……そんな経験のある方も多いのではないでしょうか。統計学の知識がないと、企画・提案の定量的な根拠を用意できず、相手を説得できない結果に終わってしまうことがあります。また、専門家にレポートを解説してもらう場面で、それぞれの数値の意味が分からず質問できなかったり、専門家の意見を鵜呑みにして社内に持ち帰るも、その内容を通訳できない状況に陥ってしまう例もあります。
どれか1つでも当てはまる方は、統計学の勉強は役に立つと思います。ただ統計学を学ぶ際に注意していただきたいことがあります。それは、ご自身の課題感に合った学習目標を設定するということ。専門家になる必要はないけれど、ビジネスシーンでデータや数字を扱いたいという方なら
- 専門家が出したレポートをざっくりと読み解けて、適切な質問や意見交換ができたり、社内で通訳できる
- 数字のトリックの可能性に気づけ、騙されないようになる
- 自分の主張に対して、統計的な根拠を付け加えられるようになる
- データから何かしらの発見やアイディアを見つけられる
この4つが目標となります。本レッスンの動画では、「学習の深さ×広さ」という視点で目標設定について解説しているので、気になる方は参照してみてください。この4つのポイントを身につけるにあたって、今回のレッスンでは「1.専門家が出したレポートをざっくりと読み解けて、適切な質問や意見交換ができたり、社内で通訳できる」の習得を目指して進めていきます。数式などは一切出てきませんので、苦手な方も安心して読んでいただけると思います。
2. 統計学の基礎用語
弊社ではデータを活用しています、と公言するためには、最低限の統計学用語を理解すること、そして誤用を防ぐことが大切です。ここでは、よく使用する用語について解説していきます。
- 「母集団(N)」:調査したい対象を含むすべての集団
これは、自分が知りたい対象に含まれるものすべてを指します。例えば男性は女性より背が高いのかについて知りたい場合は、母集団は「世の中の人すべて」となります。
次に
- 標本(サンプル)(n):母集団から無作為に抽出した集団
についてです。身長について知りたいと思っても、世界中の人の身長のデータを集めることは難しいですよね。その際は何人かのデータを集めて検証していきます。母集団の中からランダムに抽出されたデータを標本といいます。また、この標本については2つの数え方があり、
- サンプルサイズ:nの大きさ
- サンプル数:nの数
と分けられます。先程の例でいえば、サンプルサイズは1000人抽出した場合は「1000」となります。サンプル数については後述しますが、まずサンプルサイズとサンプル数は別物だという点を覚えておいてください。
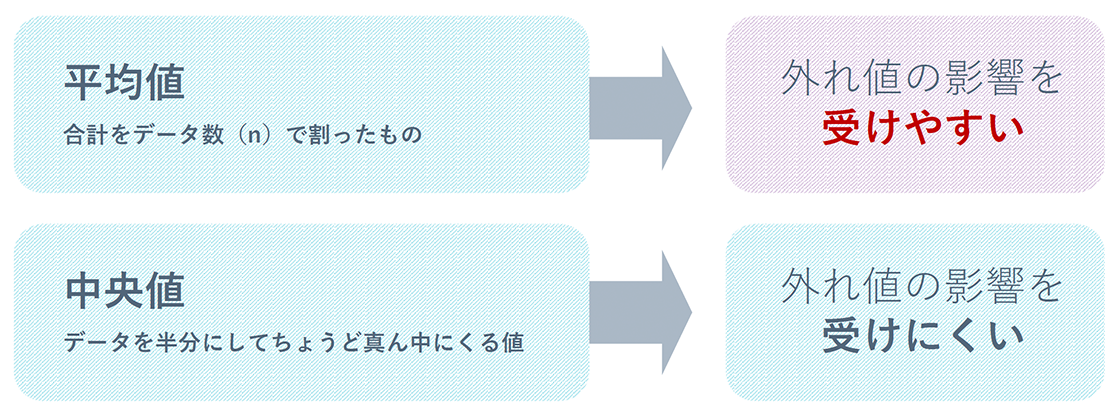
- 平均値:データを足してnで割ったもの(外れ値の影響を受ける)
- 中央値:n(サンプル)の数のちょうど真ん中にあたる値(外れ値の影響を受けにくい)
この2つの違いについても、詳しくは後述します。
- 分散:平均からのデータのバラつきを表す値(バラつきを過大評価している)
- 標準偏差:分散を現実的な値に修正したもの
分散と標準偏差については、ややこしいと思われた方もいるかもしれませんが、簡単にいえばどちらも「データの散らばり具合」を表しています。例えば、2つのグループがあって、身長の平均値がAグループもBグループも同じだった場合、
Aグループ:155㎝~165㎝の間に全員がおさまっている
Bグループ:140㎝~180㎝の間に全員がおさまっている
とすると、平均値こそ同じですが、データのばらつきはなんとなくBグループの方が大きそうですよね。この、平均値からのデータのばらつきの度合を測る指標が、分散と標準偏差です。分散と標準偏差については今回のレッスンでは詳しく説明しませんが、大事なことなので「平均値だけでなくデータのバラつきを表す指標もある」ということは覚えておいてください。

また、世の中の統計データと呼ばれるものには、
記述統計:集めたデータを分かりやすく要約したもの
推測統計:サンプルに基づいて、その母集団全体の特徴や性質を推測しようとするもの
の2つがあります。平均値、標準偏差、最大値、最小値などを記述統計といい、標本から出た結果によって母集団を推測するものが推測統計です。記述統計の例でいうと、厚生労働省の国民生活基本調査(2019)が当てはまります。これは世帯ごとの所得金額が分かるデータであり、統計学でよく使用されるヒストグラムで表されています。このデータでは平均所得金額は「552万3千円」と表されていますが、グラフを見ると平均所得以下の人数の割合は61.1%を占めています。ここから分かるように、平均値とは全体の大体真ん中の値にはなりません。この平均所得金額は高所得世帯のデータに引っ張られてしまっているのです。平均値は平均から外れたデータである外れ値の影響を受けやすいというデメリットがあります。ですので、所得や貯蓄額、単価など青天井のデータについては、中央値を使うことをおすすめします。
基礎用語を押さえた上で、次は誤用されやすい統計用語について説明します。ダントツで誤用が多いのは、サンプルサイズの意味で他の用語を使ってしまっている例です。サンプルサイズは調査するデータ数を表す用語ですが、似た言葉としてサンプル数という用語があります。例えば日本人の身長とアメリカ人の平均身長を比較したいという場合、
標本:無作為に抽出した日本人の代表者(1000人)、アメリカ人の代表者(1000人)
サンプルサイズ:2000人
サンプル数:2
となります。つまり、サンプル数は日本人とアメリカ人という括り、このグループの数である2となるのです。他にも、サンプルサイズを母数と誤用している場合もあるので、
(誤用例は動画を参照)
サンプルサイズ≠サンプル数≠母数
ということを押さえておきましょう。
3. 「統計的に有意」とは?
「統計的に有意」とはどういうことか。解説の前に「効果」とは何かについてお話しします。
効果:一言でいうと、差のこと
例えば、「このマシンを1ヶ月使用すると平均で2kg体重が落ちます」「このシステムを導入すると平均コンバージョンが10%上がります」といった広告の文言は、効果があることをうたっているものですよね。こうした効果を客観的な数字によって表し、消費者に信用してもらおうとするものについて、近年はその書き方が問題となっています。その代表例が広告です。私自信、広告代理店の方などから「論文を書くわけでもないのに統計的な証明も必要なのか?」という相談を受けることも多いのですが、判断する側(じゃあこのサービス使ってもいいかな?)と商品・サービスを提供する側(このエビデンスで十分なのか?)の双方にとって、統計的な証明は必要です。
判断する側でいえば、例えば広告出稿者がWEB広告を実施するときに、デザインAかデザインBで迷っていたとします。このとき、反応率はAの方がよかった、つまりAとBで差があったので効果があると考えるかもしれません。しかし、果たしてその差は誤差ではないのか、またサンプルサイズは適切な量かという点を明らかにしなければなりません。
この点について、効果があるかどうかの見極め方を簡略化してお伝えすると、
>効果量:効果の大きさ(差)
サンプルサイズ:その差は誤差ではないかどうか
の両面に着目することで、効果があるかどうかを判断できます。その判断基準となる値を
有意確率(p値)
といいます。統計的に分析したレポートや論文のほとんどにはこの値が掲載されています。この有意確率は0~1の値をとるのですが、この値が小さければ小さいほど、「統計的に有意」といえます(多くの場合、0.05未満で「有意」と判断します)。

ではもう一方の商品・サービスを提供する側、広告代理店が統計的な証明を必要とする例でいうと、ランディングページの審査が年々厳しくなってきており、ビフォーアフターを載せる際などは外れ値を使用しにくくなっていることが挙げられます。外れ値ではなく、広く一般にも当てはまるような確率的に無理のない範囲で掲載することが必要なのです。動画ではダイエット広告を例に説明していますので、気になる方は動画を参照してみてください。
つまり、数字を載せているからといってそれがエビデンスとは一概にはいえない。それは統計的に正しいのか?と疑ったり、提示することが必須の時代となってきていることを意識しておくようにしましょう。
上で述べた有意確率についても、効果の大きさが同じでもサンプルサイズが大きいほど有意確率が小さくなり、「統計的に有意」になりやすくなってしまうという数学的なトラップがあります。この性質を逆手にとって、主張を裏付けるために有意確率が小さくなるまでデータを集め続けるような行為はおすすめしません。大切なのは、有意確率だけではなく、そもそもどれくらいの効果があるのかという指標である効果量も併せてチェックするということです。最後に、この効果量の指標の中で分かりやすいものを1つだけ紹介したいと思います。
4. 相関関係と因果関係
相関とは、2つの値の関係性の度合いを表します。「この数字には相関がありまして…」といった言葉は皆さんもどこかで聞いたことがあると思います。例えば、身長と体重を散布図に表したとき、右肩上がりに直線的な傾向が見られたとします。このとき、身長と体重には正の相関があるといえます。逆に、一方が上がれば一方が下がるという直線的な傾向は負の相関といいます。
またこのように相関がある関係について、相関の強さを数値化したものを相関係数といいます。この相関係数こそ、効果の大きさを表す指標である効果量の一つです。相関係数はマイナス1から1の値をとり、絶対値が1に近づくほど相関が強いということを表します。目安としては、0.4~0.5以上で相関が強いというように捉えることが多いです。
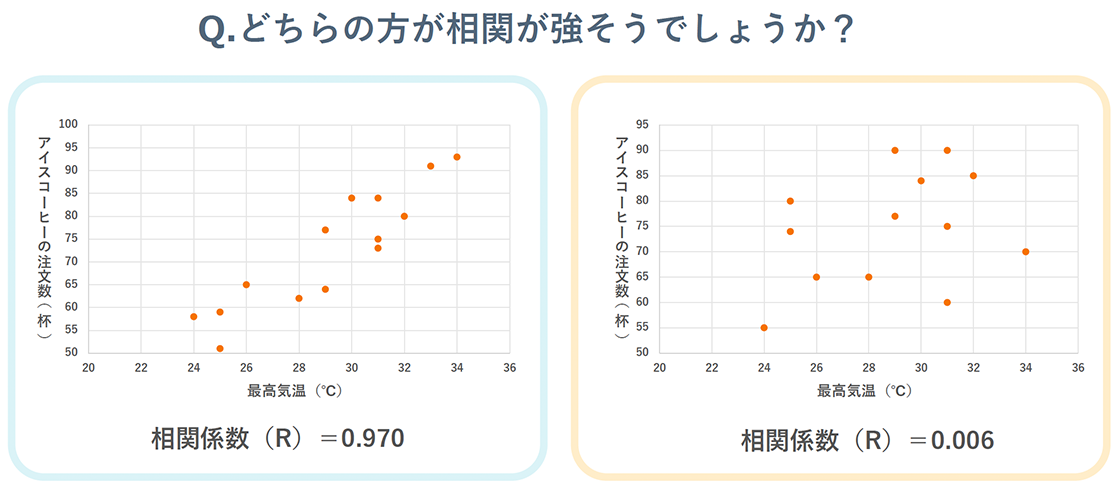
相関係数はビジネスの場面で多用されることが非常に多いのですが、注意すべき点が1つあります。それは、
相関関係≠因果関係
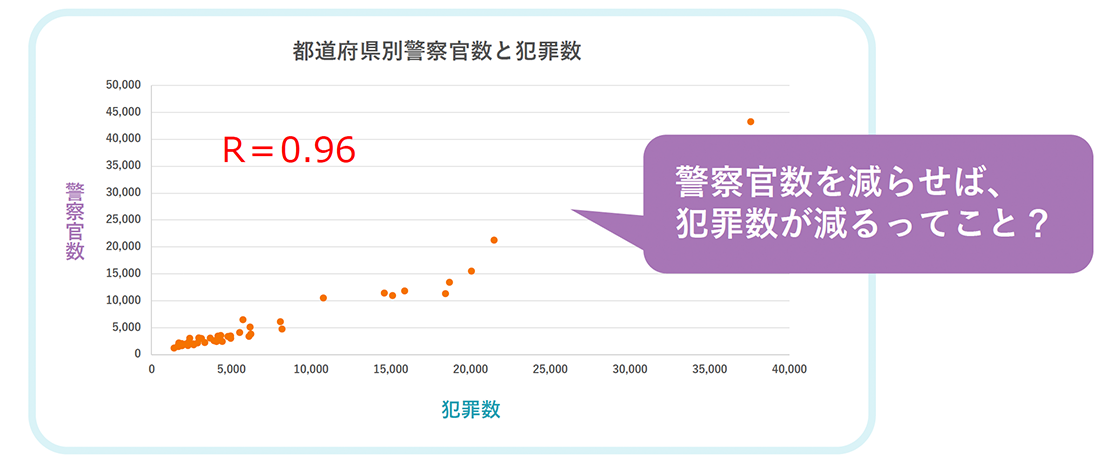
ということ。あくまで相関関係は2つの値の連動性の指標であり、一方の値を変化させるともう一方の値も変化する因果関係とは異なります。例えば、警察官の多い都道府県は犯罪件数が多いというデータを見ると、警察官数を減らせば犯罪件数が減るってこと?と考えてしまう方もいるかもしれません。しかし言い方を変えて、警察官の数を減らすという原因によって、犯罪件数が減るという結果が起きるのかといえば、そうではありません。こういった例を、
疑似相関:2つの事象に因果関係がない(かもしれない)のに、見えない要因(潜伏変数)によって因果関係があるように推測されること
と表します。この見えない要因とは、警察官数と犯罪件数の例でいえば人口に該当します。人口が多いということは必然的に警察官も犯罪件数も多くなるので、実は警察官数と犯罪件数、そして人口の3者の間で相関関係があったということです。相関関係は調べればすぐ分かるのですが、それが必ずしも因果関係になっているとは限らないので解釈には注意してください。
では、相関関係が確認されたら何をすればいいのか。それは
そこからどんな仮説が立つだろうか?を考えること
です。データから分かることのほとんどは相関関係であり、逆にいうと相関関係しか分からないことが多いです。なので、そこから因果関係の仮説を立ててみることをおすすめします。仮説や課題の立て方については、LESSON2をご覧いただければと思います。また、実際に相関関係と因果関係の検証についてはテクニックがあるのですが解説が長くなってしまうので、気になる方は別途教材をご覧ください。
今回のレッスンは以上になります。ありがとうございました。



